Antienne
Cet article est le premier d’une série de 4 articles qui vont nous permettre de voir comment il est possible de réaliser des méthodes factorielles telles qu’une ACP, AFC ou encore ACM en utilisant simultanément le langage de programmation R et l’outil de dataviz Tableau.
Dans ce premier article, il sera d’abord question de permettre à un public à profil non-statistique de comprendre l’utilité de ces méthodes factorielles pour explorer et rendre compréhensible un jeu de donnée à forte volumétrie. Cela permettra de se familiariser avec le sujet avant d’avancer dans les aspects plus techniques.
De la distribution statistique aux méthodes factorielles
La statistique, c’est l’étude des phénomènes relatifs à la collecte des données, leur traitement, leur analyse, l’interprétation des résultats et enfin leur présentation afin de les rendre compréhensibles par tout public. Elle est donc à la fois, une science, une méthode et un ensemble de techniques.
Nous allons, afin de pouvoir introduire les notions de méthodes factorielles, revenir aux raisons pour lesquelles ces méthodes ont vu le jour.
Statistiques à une variable : méthodes multivariées
On s’intéresse à un jeu de données comprenant une seule variable. Supposons les notes obtenues à un contrôle par 10 étudiants nommés de A à J.
| Student | A | B | C | D | E | F | G | H | I | J |
| Note/20 | 9 | 15 | 6 | 14 | 16 | 7 | 10 | 12 | 7 | 11 |
Nous voulons classer les élèves selon leurs notes, il est très facile de faire une représentation des différentes observations.
D’un simple coup d’œil, on constate que nous pouvons classer ces élèves en 3 groupes :
- Elèves insuffisants : A, C, F, et I
- Elèves moyens : G, H et J
- Bon élèves : B, D et E
L’exercice est très facile, nous pouvons donc établir des classes ou encore faire une représentation de la population en fonction de nos critères. On peut aller plus loin en observant les paramètres de position : minimum, maximum, médiane, moyenne ou encore les paramètres de dispersion : écart-type, variance, etc.
Nous pouvons aller plus loin en observant graphiquement les différentes distributions notifiées précédemment.
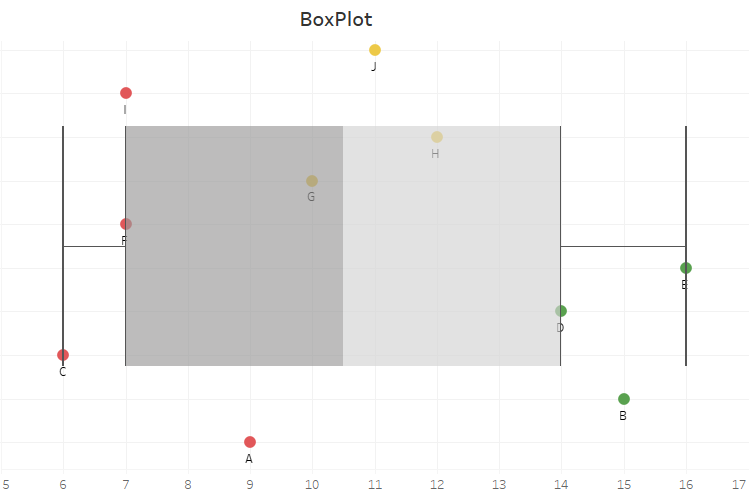
On retrouve exactement les mêmes informations. Il est donc facile lorsque l’on a une unique variable et des critères bien spécifiques d’explorer notre jeu de donnée. Cependant on est très rarement confronté à ce genre de situation.
Statistiques à deux variables : méthodes bivariées
Supposons maintenant que l’on s’intéresse à un jeu de données comprenant seulement 2 ou 3 variables numériques. Il est aussi facile de “visualiser” le jeu de données.
| Student | A | B | C | D | E | F | G | H | I | J |
| Français | 9 | 15 | 6 | 14 | 16 | 7 | 10 | 12 | 7 | 11 |
| Maths | 16 | 8 | 9 | 17 | 15 | 13 | 8 | 10 | 14 | 11 |
| PC | 15 | 10 | 10 | 16 | 16 | 12 | 8 | 9 | 15 | 11 |
Par exemple en regardant les relations entre les variables prises 2 à 2 :
- On peut essayer de caractériser la corrélation entre les variables à travers le calcul du coefficient de corrélation. Plus ce coefficient est proche en valeur absolue de 1, plus la corrélation est forte (positive ou négative).

Le résultat le plus probant est que Maths et de PC sont fortement corrélées et positivement.
On peut aussi tracer le nuage de points des variables prises 2 à 2 et voir de manière visuelle les rapprochements entre individus.
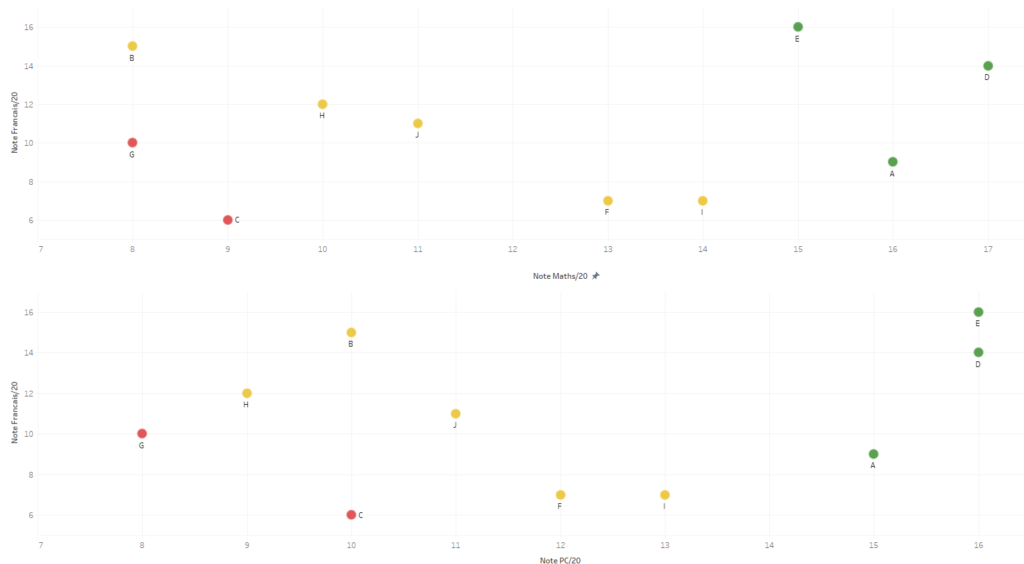
La corrélation observée entre les notes de PC et de Maths est justifiée, on peut affirmer que les notes de Maths et de PC renvoient quasiment la même information d’où la quasi ressemblance des nuages de points Francais-Maths et Francais-PC.
On peut donc refaire nos groupe d’élèves selon la moyenne obtenue et en fonction des matières scientifiques et littéraires :
- Elèves insuffisants : G et C
- Elèves moyens : H, B, F, I et J
- Bon élèves : A, D et E
Statistiques à plusieurs variables : méthodes univariées
En revanche, quand on est confronté à plusieurs variables (n>3), les méthodes statistiques univariées et bivariées ne suffisent plus à répondre à notre problème. En effet, il devient difficile de comprendre ce qui se passe dans le jeu de données…
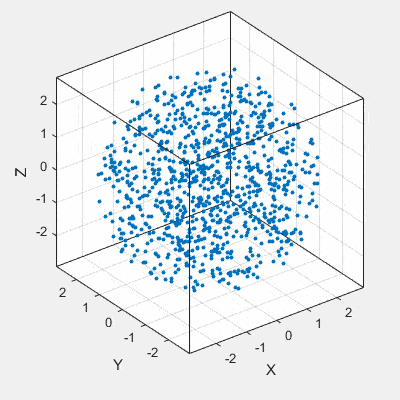
Par exemple, le graphique ci-dessus en 3D est difficilement interprétable.
Il est à priori impossible de “visualiser” le nuage de points en n dimensions d’où le recours aux méthodes factorielles.
Quelques éléments de vocabulaire nécessaires :
- Inertie : quantité d’information contenue dans un tableau de données.
- Composantes principales ou facteurs : nouveaux axes découlant d’une combinaison linéaire des variables initiales du jeu de donnée.
- Axes principaux : ensemble des composantes principales détenant le maximum d’informations.
- Valeurs propres : part d’inertie totale détenue par chaque composante principale.
Qu’est ce qu’une méthode factorielle ?
Les méthodes factorielles sont des types d’analyses de tableaux volumineux de données ayant au minimum plus de 3 variables dans le but de déterminer et de hiérarchiser les facteurs corrélés aux variables.
Communément appelée “analyse factorielle”, ces types de méthodes vont permettre de “réduire” le nombre de dimensions nécessaires à la représentation du nuage de points, c’est à dire qu’on passe des n variables initiales à p variables avec obligatoirement p strictement inférieur à n.
Comment ?
Imaginons que nous ayons un tableau de données avec 5 variables. Il est quasiment impossible de comprendre ce type de tableau à vue d’oeil ou encore de réaliser une quelconque visualisation “adéquate”.
L’analyse factorielle va donc permettre de faire une transformation du nuage de points de 5 dimensions en un ou plusieurs nuages de dimensions strictement inférieures à 5. Cette transformation permet de passer en composantes principales, composantes qui vont définir les axes d’un nouveau repère de dimensions réduites dans lequel on va projeter les points.
Que se passe t-il réellement ?
Les méthodes factorielles reposent en grande partie sur la notion d’inertie du nuage de points. On entend par inertie, la quantité d’information contenue dans un tableau de données (une inertie nulle signifie que toutes les observations sont quasi-identiques). L’idée, c’est de chercher à représenter de la manière la plus réaliste possible le nuage de points.
La première composante principale “capture” le maximum d’inertie du tableau de donnée, la seconde composante principale est un complément de la première et ainsi de suite, de manière à ce qu’il n’y ait pas de redondance d’informations entre les différentes composantes principales.
Exemple 1 : imaginons qu’on a 5 variables initiales. Ces 5 variables vont se transformer en 5 composantes principales qui vont détenir chacune un pourcentage d’information :
1ere CP = 60%, 2e CP = 26%, 3e CP = 9%, 2e CP = 4,5%, 2e CP = 0,5% et le compte fait bien 100%.
Elle est en général sous la forme d’un histogramme et chaque barre correspond à un axe :
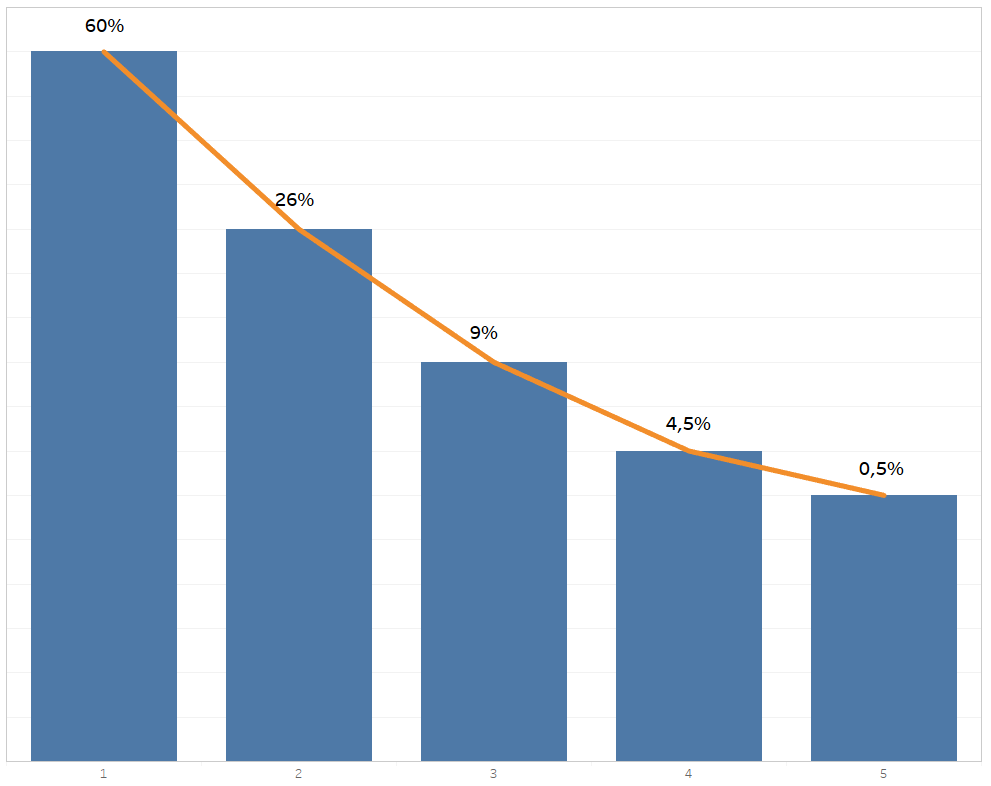
Le but est de pouvoir représenter un nuage de points tout en minimisant la perte d’information.
Avec les 5 composantes principales on a 100% d’informations mais réaliser un nuage en 5D n’est d’aucun intérêt. L’optimal serait d’avoir un nuage en 3D ou mieux en 2D.
Il faut donc observer le taux d’information que l’on arrive à récupérer :
- En choisissant de faire un graphique en 3D, nous récupérons les 3 premières composantes principales, soit 95% de l’information. Cependant le graphique en 3D sera t-il assez intuitif ?
- En choisissant de faire un graphique en 2D, on récupère 86% (soit plus de ¾ ) de l’information. De plus on a un graphique plus instructif et facilement interprétable. Ces 2 composantes sont ainsi nos axes principaux dans la construction du nuage de points.
La seconde semble la plus optimale. En la choisissant, j’ai une meilleure visibilité mais j’observe une légère perte d’information, ce qui est normal en utilisant les méthodes factorielles.
Exemple 2 : Si nous reprenons l’exemple du tableau précédent (statistiques à 2 variables), il n’y a pas grand intérêt à réaliser un nuage en 3D dans la mesure où les notes de Maths et de PC renvoient la même information (les élèves forts en Maths le sont également en PC).
La forte corrélation observée entre ces deux variables justifie pleinement que l’on récupérera moins 98% de l’information)
Exemple 3 : Un autre exemple mais graphique. Nous avons deux images aux “dimensions” différentes. Lorsqu’il y a plus de 2 dimensions il est quasi-impossible d’identifier l’animal sur la figure, alors qu’en 2D, il est facile de visualiser mentalement et d’identifier l’animal.

Cela va donc permettre d’explorer facilement l’image (ie. le jeu de donnée) et ainsi apporter des réponses plus précises. Vous aurez donc compris que l’analyse factorielle a donc pour rôle de trouver des espaces de dimensions plus petits minimisant ces déformations.
C’est cool… Mais ?
Selon le point de vue, la quantité d’informations retenue n’est pas la même. En effet, ces nouveaux axes obtenus via une combinaison linéaire d’anciennes variables capture le maximum d’inertie du tableau de données. C’est à dire que les axes principaux qui vont nous permettre de représenter le nuage de points ne récupèrent qu’une quantité de l’information (le reste de l’information est souvent “conservé” dans les axes secondaires non utilisés). On assimile cela à une perte d’information puisque ces axes sont rarement ou ne sont pas utilisés pour représenter le nuage de points.
Si l’on reprend notre image de gauche, il est difficile d’identifier de façon précise l’animal. En revanche à droite, l’identification est plus beaucoup plus claire mais on perd par exemple l’information sur le volume de l’animal (masse corporelle), information que l’on avait potentiellement dans l’image de gauche. Il y a donc toujours un léger biais dans cette réduction de dimension.
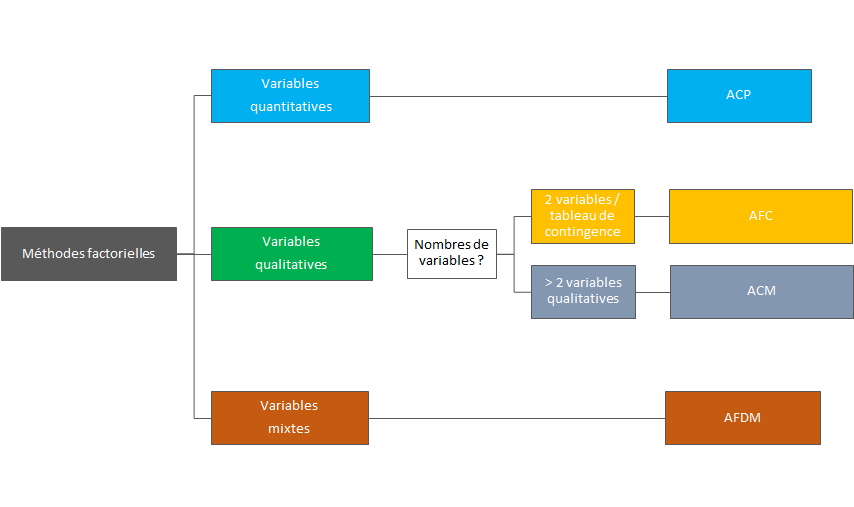
Typologie des méthodes factorielles
Ci-dessus, un résumé des méthodes factorielles avec spécification du type de variable que nous aborderons dans un second article.
Conclusion
Dans ce premier article, il a été question d’avoir une meilleure compréhension des raisons pour lesquelles nous avons recours aux méthodes factorielles : lorsque nous avons plus de 2 variables (qualitatives, quantitatives ou mixtes), les méthodes factorielles sont l’une des meilleures solutions qui se proposent à nous.
Cependant, l’utilisation de chacune de ces méthodes factorielles requiert des conditions et hypothèses spécifiques au type de donnée (qualitatif, quantitatif) à prendre en compte. Lorsque ces conditions spécifiques sont réunies, et que les constructions graphiques sont réalisées, on peut interpréter de la même manière ces méthodes.
Sachant que notre but final est de pouvoir réaliser une analyse factorielle en utilisant Tableau et R, cet article nous donne un premier choix de décision de la méthode exploratoire à utiliser rien qu’en jetant un bref coup d’oeil à notre jeu de donnée.
Dans le prochain article, nous aborderons dans un premier temps chacune des méthodes factorielles, il sera question de maîtriser les conditions et hypothèses de départ nécessaires à l’utilisation de chacune de ces méthodes puis dans un second temps, nous apprendrons à interpréter les sorties de ces méthodes factorielles.